En el año 1976, Robert M. May publicó un artículo en la revista Nature (Nature 261 459-67) titulado «Modelos matemáticos sencillos con una dinámica muy complicada» en el que destacaba la presencia de fenómenos estudiados en las ciencias biológicas, económicas o sociales que responden a modelos matemáticos representandos por ecuaciones en diferencias de primer orden con comportamientos dinámicos sorprendentes.
En el artículo citado, el autor hace un repaso detallado de estas ecuaciones y aporta numerosas referencias a casos ya estudiados. Al mismo tiempo, en la Conclusión del artículo, hace una reflexión sobre la importancia de las aplicaciones pedagógicas de estas ecuaciones en el currículo escolar.
En 1991, Heinz-Otto Peitgen, Hartmut Jürgens y Dietmar Saupe recogen la idea en un libro en dos tomos titulado Fractals for the Classroom publicado por la editorial Springer-Verlag de Nueva York en colaboración con el Consejo Nacional de Profesores de Matemáticas (NCTM en sus siglas en inglés). En la página 50 del primer tomo se preguntan qué es un modelo dinámico de población para exponer a continuación la multitud de parámetros que inciden en el tamaño de ésta, como las condiciones ambientales, la interacción con otras especies, la fertilidad, etc. No puedo por menos de reproducir aquí la «parábola medieval de los ratones y las solteronas» que los autores ponen como ilustración de la complejidad del proceso de crecimiento de la población:
«Este año hay muchos ratones en los campos. Los agricultores están muy preocupados porque a consecuencia de ello recogerán muy poco grano y en suma vendrá un periodo de pobres dotes, que hará que muchas jóvenes se queden solteras. A las solteronas les gustan mucho los gatos y la población de estos felinos crecerá dramáticamente, lo que resultará malo para la población de ratones, que decrecerá rápidamente. Esto hará felices a los agricultores que enriquecerán las dotes, se reducirán las solteronas y quedrán muy pocos gatos, con lo que volverán los ratones, y así una y otra vez.»
|
Siguiendo los argumentos de los autores citados, vamos a considerar un
cultivo de células en una placa de Petri —se llama así en honor de
su primer usuario, Julius Richard Petri (1852 - 1921) colaborador de
Robert Koch, que descubrió el bacilo de la tuberculosis— en el
que haremos recuentos periódicos de su número para obtener los valores de la población
P0, P1, P2, ...,
Pn, ... |
La variación de la población, como ya vimos al estudiar la versión diferencial de la ecuación logística, estará condicionada por la cercanía al máximo M y por una constante k relacionada con la fertilidad del cultivo. Así pues
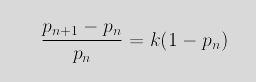
de donde resultará la ecuación logística en diferencias de primer orden que nos da la población al pasar de un momento n a un momento inmediatamente posterior n + 1:
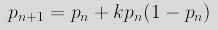
Se trata de una función cuadrática cuyo comportamiento vamos a estudiar iterándola en función del índice n para distintos valores de la constante k. Iteración de la función cuadrática